Fungsi Invers
Defenisi : Jika y = f(x) dan x = g(y) maka dikatakan g invers dari f, dan sebaliknya. Invers dari f (x) di tulis f -1(x). Jika f(x) o g(x) = 1, maka f -1(x) = g(x) dan g -1(x) = f(x)
RUMUS MASTER FUNGSI INVERS

KOMPOSISI FUNGSI
Defenisi : Suatu Fungsi f dengan daerah asal Df dan daerah hasil Rf dan fungsi g dengan daerah asal Dg dan daerah hasil Rg untuk “f komposisi g” dilambangkan f o g = {(x,y) | x ε Dg, y ε Rf dan y = f(g(x))} dimana Dg ∩ Rf ≠ Ø .
Contoh :
f(x) = 2x + 5 dan g(x) = x2 – 1, maka
f o g (x) = 2 (x2 – 1) + 5 = 2x2 – 2 + 5 = 2x2 + 3
g o f (x) = (2x+5)2 – 1 = 4x2 + 20x + 25 – 1 = 4x2 + 20x + 24
Kata kunci :
# f o g (x) artinya untuk setiap variable fungsi f disubtitusikan dengan fungsi g(x)
# g o f (x) artinya untuk setiap variable fungsi g disubtitusikan dengan fungsi f(x)
Beberapa hal penting :
# (f o g)(x) = h(x) maka f(x) = (h-1 o g)(x) dan g(x) = (f -1 o h)(x)
# (f o g)-1 = g -1 o f -1
# (f o g o h) -1 = h-1 o g-1 o f -1
RUMUS MASTER FUNGSI KOMPOSISI
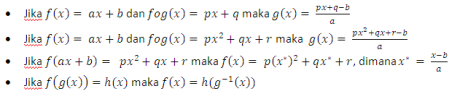
TRIK MASTER UNTUK MENENTUKAN GRAFIK YANG MEMILIKI INVERS
Ciri Grafik yang mempunyai invers
Jika dapat dibuat garis mendatar hanya memotong disatu titik (untuk satu nilai y hanya menghasilkan nilai x ). Perhatikan gambar berikut :
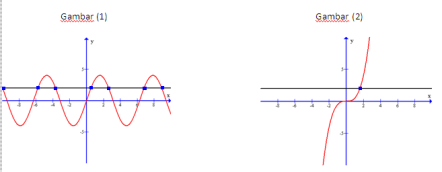
Gambar (1) tidak memiliki invers karena dapat dibuat sebuah garis mendatar dan memotong kurva pada lebih dari satu titik.
Gambar (2) memiliki invers karena garis mendatar yang dibuat hanya memotong disatu titik.
Demikian dulu kalo ada kritik dan saran silahkan diposting dalam komentar.
Defenisi : Jika y = f(x) dan x = g(y) maka dikatakan g invers dari f, dan sebaliknya. Invers dari f (x) di tulis f -1(x). Jika f(x) o g(x) = 1, maka f -1(x) = g(x) dan g -1(x) = f(x)
RUMUS MASTER FUNGSI INVERS

KOMPOSISI FUNGSI
Defenisi : Suatu Fungsi f dengan daerah asal Df dan daerah hasil Rf dan fungsi g dengan daerah asal Dg dan daerah hasil Rg untuk “f komposisi g” dilambangkan f o g = {(x,y) | x ε Dg, y ε Rf dan y = f(g(x))} dimana Dg ∩ Rf ≠ Ø .
Contoh :
f(x) = 2x + 5 dan g(x) = x2 – 1, maka
f o g (x) = 2 (x2 – 1) + 5 = 2x2 – 2 + 5 = 2x2 + 3
g o f (x) = (2x+5)2 – 1 = 4x2 + 20x + 25 – 1 = 4x2 + 20x + 24
Kata kunci :
# f o g (x) artinya untuk setiap variable fungsi f disubtitusikan dengan fungsi g(x)
# g o f (x) artinya untuk setiap variable fungsi g disubtitusikan dengan fungsi f(x)
Beberapa hal penting :
# (f o g)(x) = h(x) maka f(x) = (h-1 o g)(x) dan g(x) = (f -1 o h)(x)
# (f o g)-1 = g -1 o f -1
# (f o g o h) -1 = h-1 o g-1 o f -1
RUMUS MASTER FUNGSI KOMPOSISI
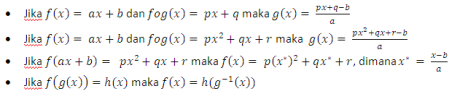
TRIK MASTER UNTUK MENENTUKAN GRAFIK YANG MEMILIKI INVERS
Ciri Grafik yang mempunyai invers
Jika dapat dibuat garis mendatar hanya memotong disatu titik (untuk satu nilai y hanya menghasilkan nilai x ). Perhatikan gambar berikut :

Gambar (1) tidak memiliki invers karena dapat dibuat sebuah garis mendatar dan memotong kurva pada lebih dari satu titik.
Gambar (2) memiliki invers karena garis mendatar yang dibuat hanya memotong disatu titik.
Demikian dulu kalo ada kritik dan saran silahkan diposting dalam komentar.

Tidak ada komentar:
Posting Komentar